なんちゃって！DCGANでコンピュータがリアルな絵を描く

最近、Deepな生成モデルが熱いです。

中でもDeep Convolutional Generative Adversarial Networks (DCGAN) は、写真並みの画像を生成できるということで、非常に有名になりました。以前書いた記事でも少し触れましたが、計算の果てに画像を生成できるってところになんか惹かれますね。

Deepな生成モデルの歴史的な流れについては以下のPFNの動画が参考になります。

www.youtube.com

ということで、DCGANの元となるGANについて説明しつつ実装し、そのあとDCGANもどきを実装し、画像生成を行おうと思います。

Generative Adversarial Nets (GAN)

　GANでは、2つのNNを学習させることによって、生成モデルを構築します。2つのNNは、それぞれDiscriminatorとGeneratorと呼ばれていて、これは競合関係にあります。

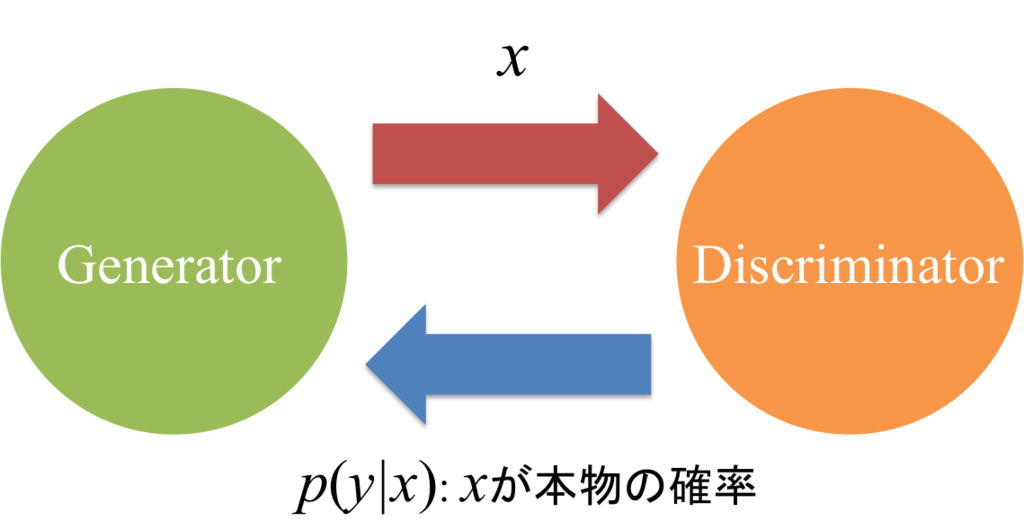
　どういうことかというと、まず、Generatorが一様乱数zからデータxを生成します。DiscriminatorはGeneratorから生成されたデータと元のデータを識別するように学習します。それに対して、Generatorは、Discriminatorが元のデータと区別できないようなデータを生成するよう学習します。このように、お互いに切磋琢磨して学習していくことで、Generatorを真の確率分布に近づけることができます。元の論文では、Generatorは偽札職人で、Discriminatorはそれを見破るものだ、という概念的な説明がなされていました。

　厳密には、まず $G(z;\theta_g)$ と $D(x;\theta_d)$ の2つのネットワークを用意します。ここで、 $\theta_g$ と $\theta_d$ はそれぞれの学習すべきパラメータを示します。このとき、 $D(x;\theta_d)$ は、xが真の確率分布 $p_{delta}(x)$ とGeneratorの確率分布 $p_g(x)$ のどちらから生成されたのかを識別するような出力を得たいのでデータxを入力とした時の $D(x;\theta_d)$ の最適な値は次式のようになります。

$D^{*}(x)=\cfrac{p_{delta}(x)}{p_{delta}(x)+p_g(x)}$

このとき、 $D(x)$ はxが $p_{delta}(x)$ から生成される確率を表し、 $1-D(G(z))$ は $p_g(x)$ から生成された確率を表すことになります。ここで、 $p_{delta}$ と $p_g$ の $JS$ ダイバージェンスを考えます。

${ \displaystyle \begin{eqnarray}2JS(p_{delta}||p_g)&=&KL(p_{delta}||\frac{p_{delta}+p_g}{2})+KL(p_g||\frac{p_{delta}+p_g}{2})\\\\ &=&E_{x\sim p_{delta}}log\frac{2p_{delta}}{p_{delta}+p_g}+E_{x\sim p_g}log\frac{2p_g}{p_{delta}+p_g}\end{eqnarray} }$

これを先に定義した $D(x)$ を用いて表すと以下のようになります。

${\displaystyle \begin{eqnarray}2JS(p_{delta}||p_g)&=&E_{x\sim p_{delta}}log\frac{p_{delta}}{p_{delta}+p_g}+E_{x\sim p_g}log\frac{p_g}{p_{delta}+p_g}+log4\\ \\&=&E_{x\sim p_{delta}}log D(x)+E_{x\sim p_g}log(1-D(x))+log4\end{eqnarray} }$

Discriminatorとしては、これを最大化するように、また、Generatorとしては、これを最小化するように $\theta_d$ と $\theta_g$ をそれぞれ学習したいです。よって、パラメータの更新はそれぞれ以下のようになります。

${ \displaystyle \begin{eqnarray} \theta_d &\leftarrow& \theta_d + \eta \nabla_{\theta_d} \{ E_{x \sim p_{delta}} log D(x)+E_{x \sim p_g} log (1-D(G(z;\theta_g))) \}\\\\ \theta_g &\leftarrow& \theta_g - \eta \nabla_{\theta_g} E_{z \sim p_z} log (1-D(G(z);\theta_d)) \end{eqnarray}}$

ここで、 $\eta$ は学習率です。ただ、実際にはこの更新ではうまく学習ができないらしく、その原因としては、データを生成するタスクよりも分類するタスクが容易であることが元の論文で指摘されています。つまり、 $D$ の学習が早く進むため、 $1-D(x)$ がすごく小さな値になり、 $G$ の勾配も小さくなって良い結果がでないらしいです。そのため、論文では $G$ の更新を少しいじって学習させています。具体的には次式の通りで、 $log (1-D(G(z)))$ を最小化する代わりに $log D(G(z))$ を最大化するよう学習しています。

${ \displaystyle \theta_g \leftarrow \theta_g + \eta \nabla_{\theta_g} E_{z \sim p_z} log D(G(z);\theta_d) }$

しかし、この式は論理的に説明できないということがこちらの記事で指摘されていて、もう少しこの式をいじることで $KL$ ダイバージェンスの最小化として解釈できると説明されています。具体的には次式のように変形します。

${ \displaystyle \theta_g \leftarrow \theta_g + \eta \nabla_{\theta_g} E_{z \sim p_z} log \cfrac{D(G(z);\theta_d)}{1-D(G(z))} }$

ここで、 $D$ の理想的な値の定義を思い出してみると、次式のように変形でき、これは $p_g$ と $p_{delta}$ 間の $KL$ ダイバージェンスを最小化していると説明することができます。

${ \displaystyle \begin{eqnarray} \theta_g &\leftarrow& \theta_g - \eta \nabla_{\theta_g} E_{x \sim p_g} log \cfrac{p_g}{p_{delta}}\\\\ \theta_g &\leftarrow& \theta_g - \eta \nabla_{\theta_g} KL(p_g||p_{delta}) \end{eqnarray} }$

となります。こっちのほうがなんかすっきりしますね。まあ、今回は元の論文で示されている手法で実装を行っていますが...。

実践

それでは、GANを利用してデータ生成を行ってみます。利用するネットワークは3層の多層パーセプトロンです。

- 正規分布

まずは、正規分布に基づく乱数をGを利用して近似してみます。

上の図は学習の過程を示しています。最初にランダムに定めた200個の100次元の値をGの入力として得た値を学習するごとに図示したものです。これからわかるように、最初はランダムな配置となっていますが、学習するにつれて正規分布的な広がりを持つようになっています。結果として、一様分布に基づく乱数zを用いてG(z)を計算すると、それが正規分布に基づく乱数になっているということになります。

- MNIST

次に手書き数字のデータセットであるMNISTを利用して、手書き数字っぽい画像を生成してみます。

上の図は、正規分布の場合と同様に、学習の過程を示しています。今回は100次元の値を1つだけ最初に定め、そのepochごとの出力を画像として表しました。なんとなく数字っぽいものを学習していることがわかりますね。

Deep Convolutional Generative Adversarial Network (DCGAN)

　DCGANは、その名の通り、GANのそれぞれのネットワークをdeepにしたものです。これによってほとんど写真と見分けがつかないほどの精度の画像を生成することが可能となりました。

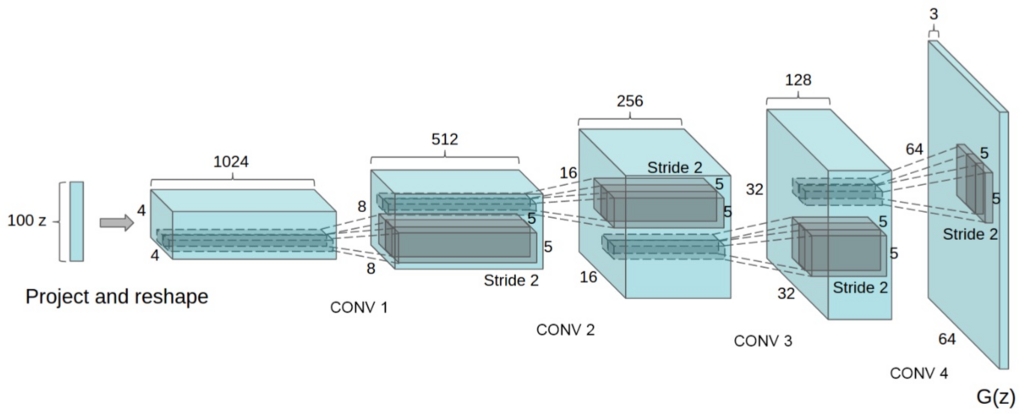
DCGANのネットワーク構造(論文より引用)

　この論文の成果としては、ネットワークをdeepにしてもそこそこ安定して学習を進めることができるような条件を示したとろこにあります。また、学習したDiscriminatorで生成した特徴量を利用した画像認識問題も良い精度を示しているようです。その安定して学習できるような条件は以下のようになっています。

すべてのプーリング層の代わりにストライドありの畳み込み層を使う
バッチ正規化をすべての層に対して行う
隠れ層の全結合をなくす
Generatorの活性化関数は出力層はtanh、それ以外はReLuを使う
Discriminatorのすべての層の活性関数にLeakyReLuを使う

実装上の細い学習パラメータ等はこちらやこちらを参考にさせていただきました。

実践

　私が実装したDCGANは、厳密には上記の論文で示されているネットワークの構造とは少し違っていて、論文のものと比べてパラメータの数が結構少なくなっています。というか層は3つしかないので、そもそもdeepかどうか怪しいです。ということで「なんちゃってDCGAN」と呼んでいます。まあ、これはCPUで早く学習して欲しいということで、そういう構造にしました。

　それでは、「なんちゃってDCGAN」でリアルな絵を描かせてみましょう。学習した結果がこちらです。

f:id:YasuKe:20160614143405p:plain:w200 f:id:YasuKe:20160614143408p:plain:w200 f:id:YasuKe:20160614143414p:plain:w200 f:id:YasuKe:20160614143413p:plain:w200 f:id:YasuKe:20160614143416p:plain:w200 f:id:YasuKe:20160614143420p:plain:w200 f:id:YasuKe:20160614143406p:plain:w200 f:id:YasuKe:20160614143415p:plain:w200

おお...！そこそこいいんじゃないでしょうか！ところどころグロテスクなものもありますが、とりあえず顔っぽいものが生成されているのがわかります。しかも割とくっきりしていて、ぼやけたりはしてません。というところで、DCGANの威力が垣間見れたかなと思います。学習にはskit-learnで用意されているこちらのデータセットのメソッドを利用しました。やっぱり、計算することでこういったことができるのはすごいですね！

GitHubに今回実装したDCGANのソースコードをアップしています。よかったらどうぞ。
GitHub - YasukeXXX/DCGAN

最後に

　これまで見てきたように、GANは非常に素晴らしい成果を上げています。しかし、問題もかなりあって、それについてはPFNの岡野原さんのスライドが参考になります。

現在のDNNにおける未解決問題 from Daisuke Okanohara

www.slideshare.net

また、Adversarial AutoencodersとかAdversarial Learned Inferenceとかいろいろ出てきてたりしてこの辺の研究が盛り上がっていきそうです。まあ、Deepにするだけでなんでも性能上がっちゃって怖いですが、この流れは止まらないどころか加速していくでしょうね。